Despite of the fact that 4-dimensional manifolds together with 3-dimensional manifolds are the most fundamental and important objects in geometry and topology and topologists had great achievements in 1960's, there has been little known on 4-manifolds, in particular on smooth and symplectic 4-manifolds, until 1982. In 1982, M. Freedman classified completely simply connected topological 4-manifolds using intersection forms and S. Donaldson introduced gauge theory to show that some topological 4-manifolds do not admit a smooth structure. Since then, there has been a great progress in smooth and symplectic 4-manifolds mainly due to Donaldson invariants, Seiberg-Witten invariants and Gromov-Witten invariants. But the complete understanding of 4-manifolds is far from reach, and it is still one of the most active research areas in geometry and topology.
My main research interest in this area is the geography problems of simply connected closed smooth (symplectic, complex) 4-manifolds. The classical invariants of a simply connected closed 4-manifold are encoded by its intersection form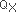 , a unimodular symmetric bilinear pairing on H2(X : Z). M. Freedman proved that a simply connected closed 4-manifold is determined up to homeomorphism by
, a unimodular symmetric bilinear pairing on H2(X : Z). M. Freedman proved that a simply connected closed 4-manifold is determined up to homeomorphism by 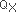 . But it turned out that the situation is strikingly different in the smooth (symplectic, complex) category mainly due to S. Donaldson. That is, it has been known that only some unimodular symmetric bilinear integral forms are realized as the intersection form of a simply connected smooth (symplectic, complex) 4-manifold, and there are many examples of infinite classes of distinct simply connected smooth (symplectic, complex) 4-manifolds which are mutually homeomorphic. Hence it is a fundamental question in the study of 4-manifolds to determine which unimodular symmetric bilinear integral forms are realized as the intersection form of a simply connected smooth (symplectic, complex) 4-manifold - called a existence problem, and how many distinct smooth (symplectic, complex) structures exist on it - called a uniqueness problem. Geometers and topologists call these ‘geography problems of 4-manifolds’.
. But it turned out that the situation is strikingly different in the smooth (symplectic, complex) category mainly due to S. Donaldson. That is, it has been known that only some unimodular symmetric bilinear integral forms are realized as the intersection form of a simply connected smooth (symplectic, complex) 4-manifold, and there are many examples of infinite classes of distinct simply connected smooth (symplectic, complex) 4-manifolds which are mutually homeomorphic. Hence it is a fundamental question in the study of 4-manifolds to determine which unimodular symmetric bilinear integral forms are realized as the intersection form of a simply connected smooth (symplectic, complex) 4-manifold - called a existence problem, and how many distinct smooth (symplectic, complex) structures exist on it - called a uniqueness problem. Geometers and topologists call these ‘geography problems of 4-manifolds’.
Since I got a Ph. D. with a thesis, Seiberg-Witten invariants of rational blow-downs and geography problems of irreducible 4-manifolds, I have contributed to the study of 4-manifolds by publishing about 30 papers - most of them are average as usual and a few of them are major breakthrough for the development of 4-manifolds theory. In this talk, I'd like to survey what I have done, what I have been doing and what I want to do in near future.
My main research interest in this area is the geography problems of simply connected closed smooth (symplectic, complex) 4-manifolds. The classical invariants of a simply connected closed 4-manifold are encoded by its intersection form
Since I got a Ph. D. with a thesis, Seiberg-Witten invariants of rational blow-downs and geography problems of irreducible 4-manifolds, I have contributed to the study of 4-manifolds by publishing about 30 papers - most of them are average as usual and a few of them are major breakthrough for the development of 4-manifolds theory. In this talk, I'd like to survey what I have done, what I have been doing and what I want to do in near future.

